Abstract Algebra II
This course covers the basic definitions and properties of rings, ideal, homomorphism and quotient ring, the isomorphism theorems for rings, maximal and prime ideals, polynomial rings, unique factorization, principal ideal domains and Euclidean domains, rings of fractions, irreducible polynomials, and Galois theory of rings.
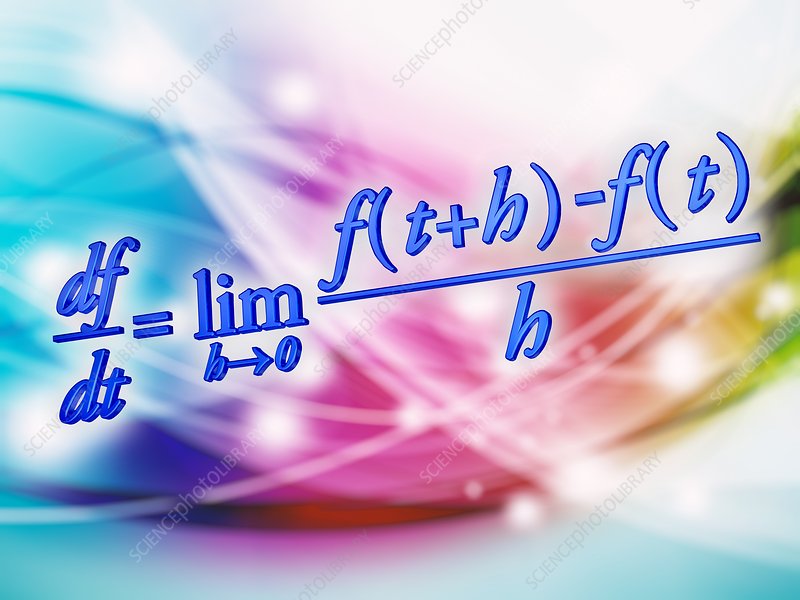
Calculus I
This is the first course in calculus. It covers limits, continuity, derivatives of algebraic and transcendental functions. This will help the students evaluate, compute, distinguish, solve and apply the different topics of calculus.

Calculus III
This course is the third and the last of a series of three calculus course. This course covers vectors in the plane and in space, vector-valued functions, and the calculus of vector fields.

Complex Analysis
This course provides an in-depth exploration of complex numbers and the complex plane, covering foundational concepts such as the Cauchy-Riemann equations, Riemann surfaces, and conformal mappings. Students will delve into advanced topics including infinite series, complex integration, singularities, and the Cauchy integral theorem. The course also emphasizes the study of residue theory and its applications in complex analysis, offering a comprehensive understanding of both theoretical and practical aspects of the subject.

Number Theory
This course intends to facilitate understanding of number theoretic concepts and properties as well as enhance skills in
employing different proving techniques which are useful in most areas in mathematics. Generally, it entails exploration, seeking
of patterns, generating and proving conjectures as students engage in mathematical investigations. Topics include divisibility,
prime numbers, unique factorization, Diophantine equations, linear congruences, and multiplicative functions.